Assume we have a logistic regression of the form $\beta_0 + \beta_1 x$, and for value $x_0$ we predict success probability $p(x_0)$. Which of the following is correct?

a) $p(x_0 + 1) = B_1 + p(x_0)$

b) $\frac{ p(x_0 + 1) }{ 1 – p(x_0 + 1) } = \exp(\beta_1) \frac{p(x_0) }{1 – p(x_0)}$

c) $p(x_0 + 1) = \Phi(B_0 + B_1( x_0 + 1))$

Assume we run a logistic regression on the 1-dimensional data below. What happens?

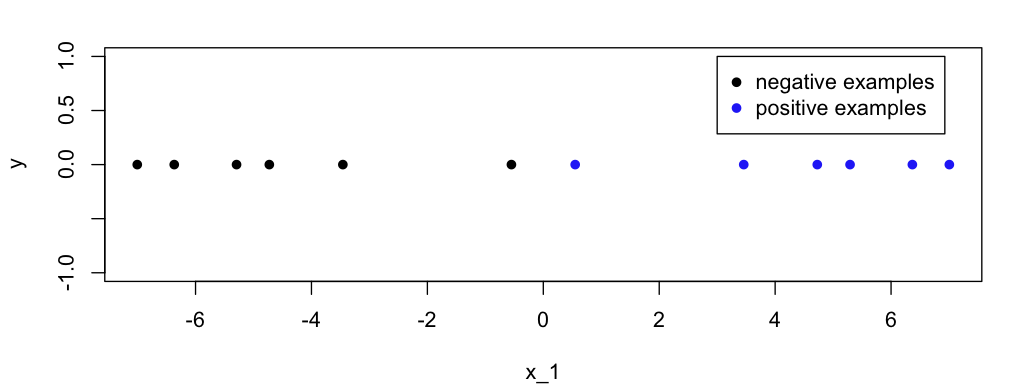
a) $– \infty < B_0 < \infty; B_1 \rightarrow \infty$

b) $\beta_0 = 0$, $\beta_1 = 0$

c) $\beta_0 = 0$; $\beta_1 \rightarrow –\infty$

d) none of the above